多くの研究ではxZ検定が行われる 。 なお、X2検定ではなく各群の比率(表1− 1 の場合、3歳児群 、 4歳児群それぞれの正答率) ・56一 L Fisher' s exact testの凵本語表記は、「Fisherの直説法」 以外に「Fisherの直接正確確率」、もしくは単に「正確確率」本サイトは、2way Contingency Table Analysisを著者の許可を得て日本語翻訳したものです(07年)。 このページは2×2テーブルから様々な統計を計算します。 イエーツ補正のカイ2乗検定、MantelHaenszel検定、Fishser正確確率検定、その他の様々な2x2分割に関連した検定について計算するもの 名古屋市立大学大学院医学研究科 非常勤講師 薬学博士 松本一彦 第8話でFisher正確検定の両側検定について、統計ソフトによって手法はまちまちであることを述べました。今回はさらに、片側検定の使い方について統計家のニュアンスが異なることと検証的な臨床試験と探索的な前臨床試

カイ二乗 X2 とfisherの検定 化審法 動物数 5 Vs 5 7 Vs 7 Or 12 Vs 12を考える Ppt Download
フィッシャーの正確確率検定 エクセル 関数
フィッシャーの正確確率検定 エクセル 関数- フィッシャーの正確確率検定では、それぞれの場合の発生確率から、実際に観測されたデータの珍しさを検定する 検定を行う場合には、あらかじめ「帰無仮説」を設定する必要があります。 例えば「本物のクスリと偽物のクスリは、 有効性に差がない フィッシャーの正確確率検定は、データが 2 つのカテゴリに分けられるとき、その 2 つのカテゴリが互いに独立しているかどうかを検定する方法の一つである。 独立性の検定については、 カイ二乗検定 を用いることも可能だが、標本数が少ない時




Fisherの正確確率検定 Study Channel
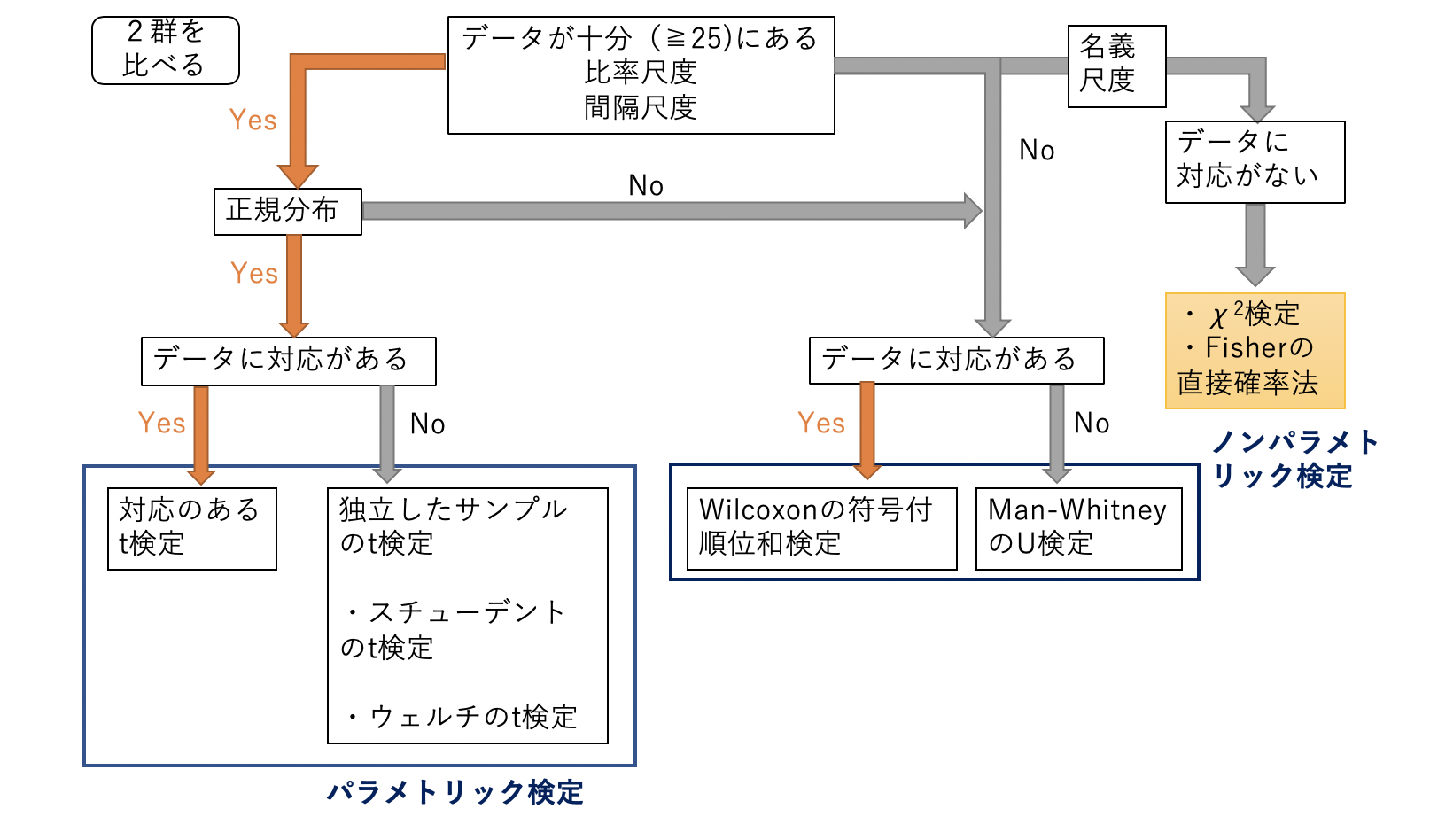
ftestの値は両側確率であるため、片側確率は半分の"0275"になります。有意水準を5%とすると、0275 > 005 となり、2つのグループでの有意差は無いと判断でき、仮説は棄却されず、分散は同じであると言えます。 f検定をする 続いて、先の条件の値に変更します。 今回は「2群間を比べる」検定のひとつである 「カイ2乗(χ 2)検定」「フィッシャー(Fisher)の正確検定(直接確率法)」 について実践してみたいと思います。 「カイ2乗(χ 2)検定」は聞いたことありますか? 学会発表などでも使いやすい検定ですので、聞いたことがある方も多いとエクセルのvbaを使って作成した、フィッシャーの直接確率計算のプログラムです。 使い方 1終了したいときには、「excel終了」ボタンを押して下さい。 2プログラムをアンインストール(削除)するときには、ホルダー全体を削除して下さい。 注意事項
なお正確確率においては片側は両側を2でわった値ではない。片側p値は観測値以下(または以上)の生起確率をすべて足したものである。 pvalue ← 1 sum(実測値の生起確率よりも大きい確率) 2*2(自由度1)のクロス集計表で正確確率を求める関数サンプル検定法には、フィッシャー(Fisher)の正確検定とピアソン(Pearson)のχ 2 検定があります(「独立性の検定」とも言います)。 帰無仮説H 0 :A 1 (A 2 )の発生する確率は、B 1 とB 2 で同じであるFisher (フィッシャー) の正確確率検定は、名義尺度のデータで、頻度の偏りを調べたい時に、かつPearsonのカイ二乗検定が使えない場合に用います。 臨床研究では、極端に標本数が少ない場合にPearsonのカイ二乗検定の代わりに登場することが多い検定です。
説明 両側確率p値の求め方については,Pearsonのカイ二乗法とFisherが示した方法があります。 2つの方法によるp値は,ほとんどの場合に同じですが,異なることもあります。 jsSTARではFisherが示した方法で求めています。 オッズ比検定では,いずれかの観測値に 0 Fisherの正確検定(以下、Fisher検定とする)とは、 カイ二乗検定 のような漸近的性質を使わず、超幾何分布とよばれる確率分布に基づいて「正確な」確率計算を行うことが名称の由来だといわれている。 カイ二乗検定 はサンプルサイズがある程度大きくフィッシャーの正確確率検定でやっていることは、カイ二乗検定と一緒 フィッシャーの正確確率検定。 t検定とかf検定とかと比べると、やたら長い名前です。 その仰々しい名前から、「なんか難しそう・・・」とあなたは思っているかもしれませんね。




フィッシャーの正確確率 株式会社ダイナコム




フィッシャーの正確確率検定 情報リテラシー
エクセルを使って、フィッシャーの正確確率検定(2x2)を行いたいと思っています。 たとえば、 アンケート総数 男 10人 女 00人 の中で、 犯罪歴 男 5人 女 1人 という回答が得られた場合、 男女間で犯罪を犯している確率に有意差はあるかどうかを調べるに フィッシャーの正確検定 (Fisher's exact test)は、フィッシャーの直接確率法とも呼ばれるもので、2x2の分割表が得られたときに有意差があるかないかを調べるときに使われます。 χ2乗検定も同じ目的で使われますが、違いはデータの個数が少ないかどうかFisher の正確確率検定を Excel を使って計算するとは?統計学用語。 質問:Excel で,a=63, b=79, c=80, d=64 のようなデータに対して Fisher's exact test の計算をしようとすると,#NUM!と表示されて途中からおかしくなって
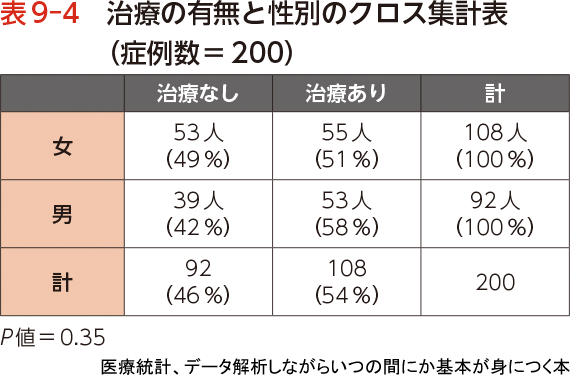



医療統計 データ解析しながらいつの間にか基本が身につく本 Stataを使ってやさしく解説 羊土社




Ezrでfisherの正確検定を行う方法 深kokyu
Ezrでカイ二乗検定を実施するために必要となるデータを読み込む方法 まずは、カイ二乗検定を実施するために必要なデータを解説します。 カイ二乗検定は、分割表を検定する方法の1つでした。 カイ二乗検定のほかに分割表を検定するのは、フィッシャーの正確確率検定でしたね。フィッシャーの正確確率検定(フィッシャーのせいかくかくりつけんてい、英 Fisher's exact test )は、標本の大きさが小さい場合に、2つのカテゴリーに分類されたデータの分析に用いられる統計学的検定法である 。 フィッシャーの直接確率検定ともいう。名称は考案者ロナルド・フィッシャー (有意水準を005として)3群で3回検定を行うと、有意とならない確率は (1005)×(1005)×(1005)=086となり、有意水準が014に上昇する。 統計検定を理解せずに使っている人のために III JStage と言われても、なぜ同時確率になるのか?



Ai U Hyogo Ac Jp



クロス集計 Spssの使い方
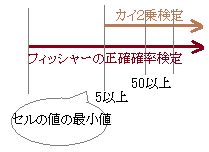
分割表の検定 分割表の検定にピアソンの$ \chi^2$検定を用いることができるのは、基本的に総数が大きい場合です。 その他の場合は、 フィッシャーの正確確率検定 (Fisher's exact test)を用いて検定します。 なお、ピアソンの$ \chi^2$検定を用いることができる場合でも、フィッシャーの正確確率 χ2乗検定が用いることができないのであればどうすればよいか.そこで出てくるのがFisher正確確率検定(Fisher's exact probability test)である.Fisherは有意水準としてp=005をカットオフとすることを最初に使用した人物として知られ,その後はこの005が慣習化さ はじめに みなさんは"フィッシャーの正確確率検定"と"カイ2乗検定"という言葉を聞いて, どちらの方がより正確そうだと思いますか? 答えは, 「2者は比較できない」です。 しかし, 生物統計ではこの2者のどちらかを使うかがしばしば問題になり, 「カイ2乗検定が役に立たないシ




フィッシャーの正確確率検定とは Youtube




Fisher正確検定 Catchapp Iphoneアプリ Ipadアプリ検索
## 計数データにおけるフィッシャーの正確確率検定 ## ## データ x ## P値 = ## 対立仮説 オッズ比は,1ではない ## 95 パーセント信頼区間 ## 標本推定値 ## オッズ比 ## \(p\) 値は 0038 であり,独立性の検定でイエーツの連続性の Rの練習 fishertest ()でメモリが足りなくなる ちょっとしたデータをカイ二乗検定しようとすると、往々にして、期待度数が5に満たないセルが存在するせいで警告が出ます。 > print ( d) Group1 Group2 Item1 3 2 Item2 9 12 Item3 32 41フィッシャーの正確確率検定の場合 ①新しく開発された新薬aが従来薬bよりも有効であることを示す場合 この場合、「新薬 > 従来薬」という結果があるか否か、という検定であるので、片側検定を行い




Excel Vbaでフィッシャーの正確検定ができる関数を作ってみた1 静粛に 只今統計勉強中




データ分析 グラフ作成14 眼科医と眼科専門mrのためのデータ分析あれこれ
フィッシャーの正確確率検定(フィッシャーのせいかくかくりつけんてい、英 Fisher's exact test )は、標本の大きさが小さい場合に、2つのカテゴリーに分類されたデータの分析に用いられる統計学的検定法である 。 フィッシャーの直接確率検定ともいう。名称は考案者ロナルド・フィッシャーカイ二乗検定を行うときの注意 条件間に対応のないケースのみ使用可能 ⇒対応がある場合、マクネマー検定、コクランのq検定 など、他の検定を使う。 観測度数が少ない(n適合度検定(4) 仮説検定を考えるにあたり,最も困難な部分は検定統計量が帰無仮説の下で従う確率分布の導 出である.検定統計量𝑋02が帰無仮説の下で自由度 −𝑟−1のカイ二乗分布に従うことを示す ( =2,𝑟=0の場合) 𝑋0 2= 𝑋1− 2



Amed Go Jp
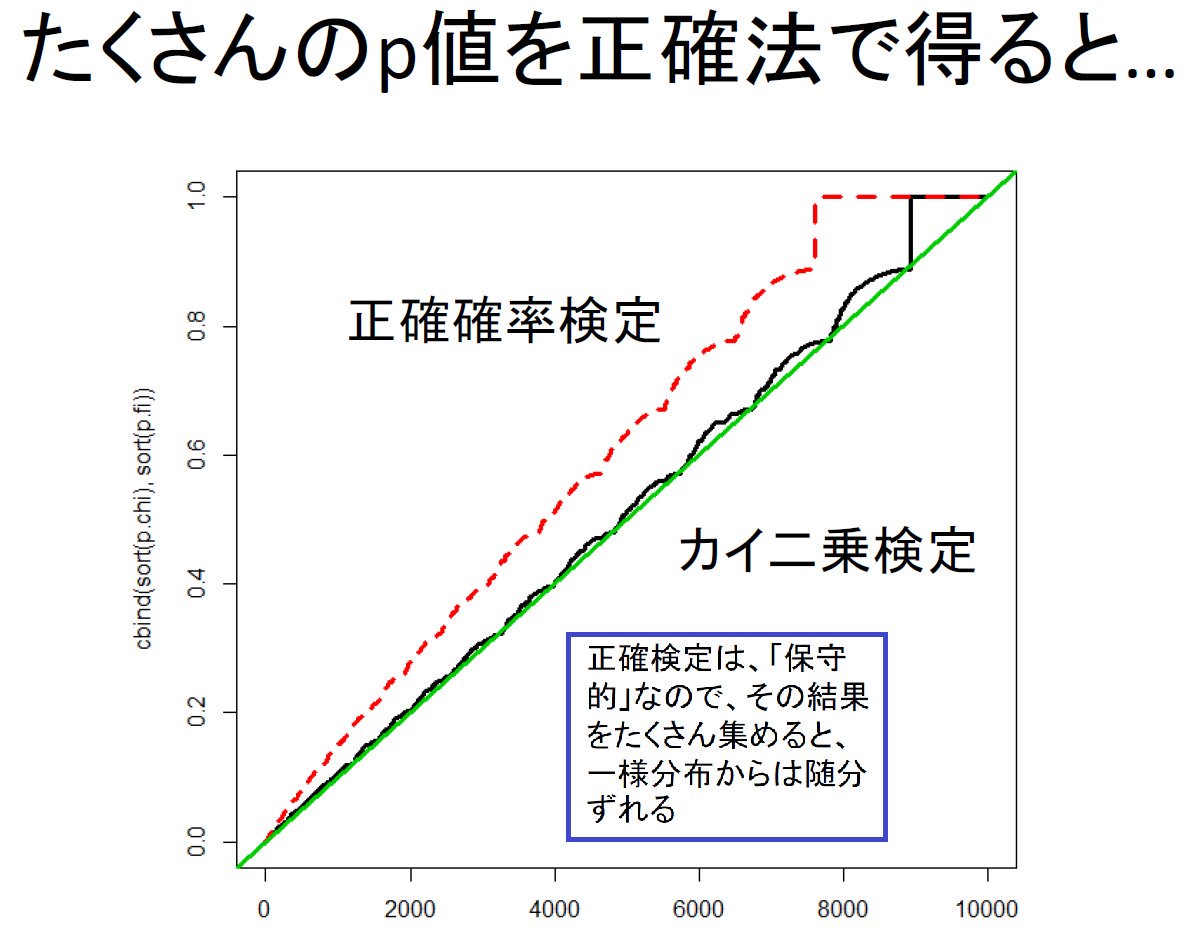



黒木玄 Gen Kuroki 統計 同様のプロット については以下のリンク先を参照 ただし 縦軸と横軸が入れ替わっている Poisson分布 4だけではなく 四項分布 二項分布 2でサンプルを生成した場合も同様である Fisherの正確検定でp値が0 05以下になる確率
5 第1 章 クロス集計表としてまとめられたデータの取 り扱い 11 2×2 分割表の場合 表11 に示すような2×2 分割表は,111 および112 に示すような2 通りの調査で得られる。 見かけ上はいずれの調査法で得られたものかは分からないが,概念的には異なることを理解しておくべきであ 手順 最初に下図の表を作成します。 期待値通りに全員にあたりが出たとします。 H2セルに下記の数式を入力します。 数式を確定すると、H2セルには、"1" が表示されます。 期待値と観測値が全く同じため、適合度は100%となります。 続いて、条件をフィッシャーの正確確率検定を使用して、インフルエンザ予防接種を受けることとインフルエンザの感染の間に無作為ではない関連性があるかどうかを判定します。 h = fishertest (x) h = logical 0 返された検定の判定 h = 0 は、既定の 5% の有意水準において



Ai U Hyogo Ac Jp




Fisherの正確確率検定 は正確ではない



フィッシャーの正確確率検定 Fisher Sexacttes Yahoo 知恵袋
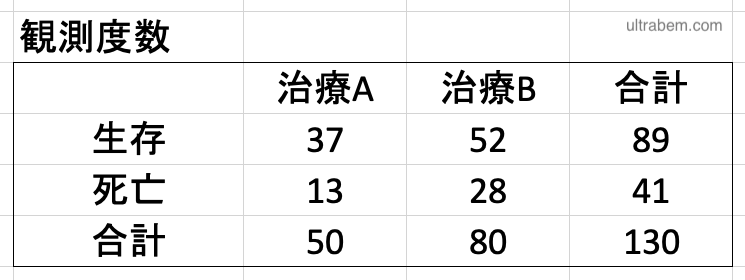



カイ二乗検定 独立性の検定 原理と Excel による解析




Rでフィッシャーの正確確率検定fisher Test Youtube




Excel Vbaで3群以上の比率の差の多重検定ができるマクロを作ってみた1 静粛に 只今統計勉強中




第4講 分割表の検定と論文表現




Fisherの正確確率検定 Study Channel
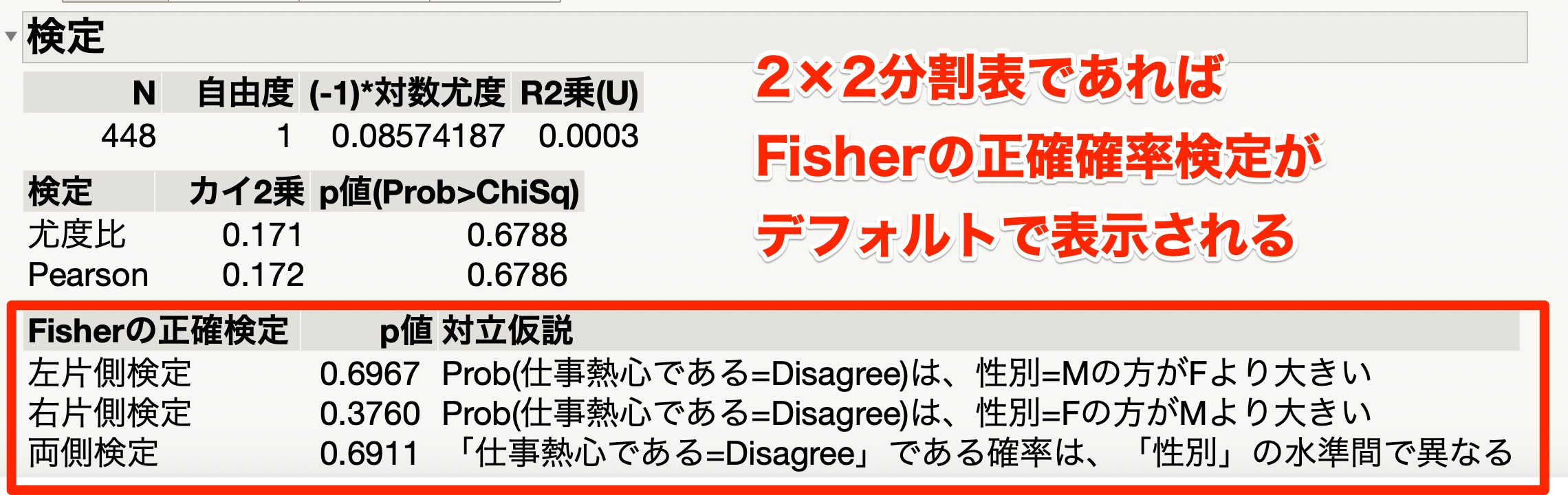



Jmpでカイ二乗検定を実施する方法 フィッシャーの正確確率検定も いちばんやさしい 医療統計




Ezrでfisherの正確検定を行う方法 深kokyu




フィッシャーの正確確率検定と カイ二乗検定の違いは何ですか どっちを使えば良いか分かりません Peing 質問箱
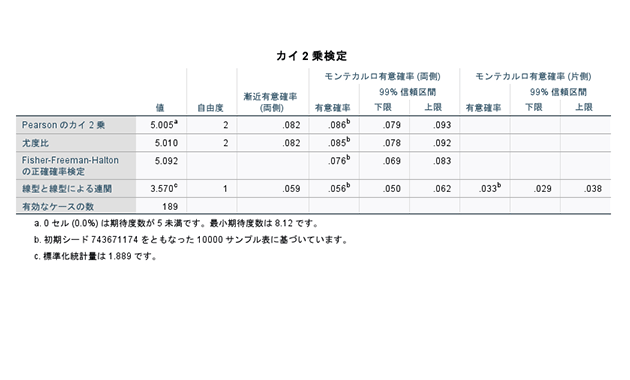



Ibm Spss Exact Tests 製品情報 小サンプルでの正確有意確率
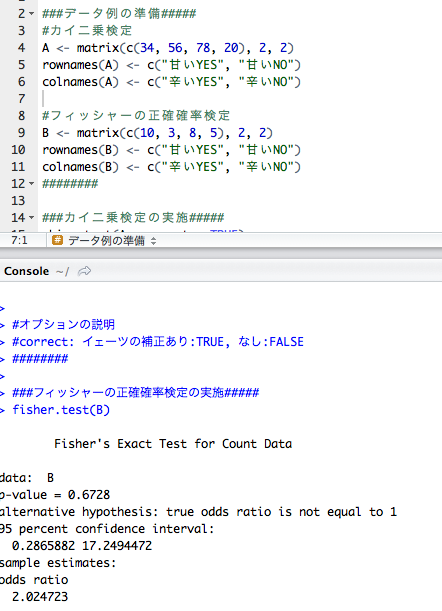



Rとウェブ解析 カイ二乗検定とフィッシャーの正確確率検定のコマンド紹介
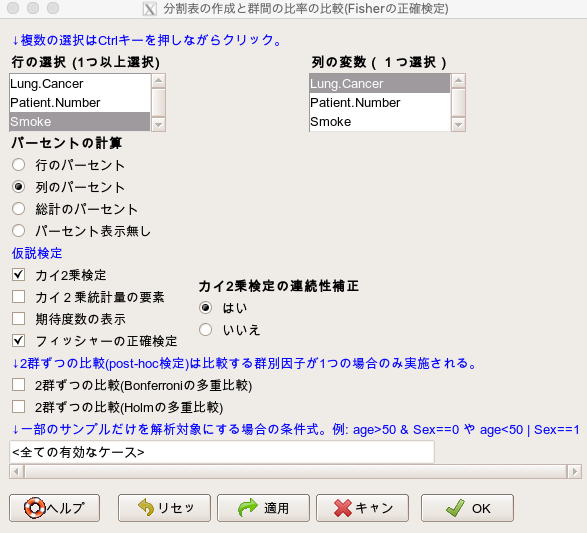



Ezrでカイ二乗検定とフィッシャーの正確検定の実施方法 分割表でクロス集計 いちばんやさしい 医療統計
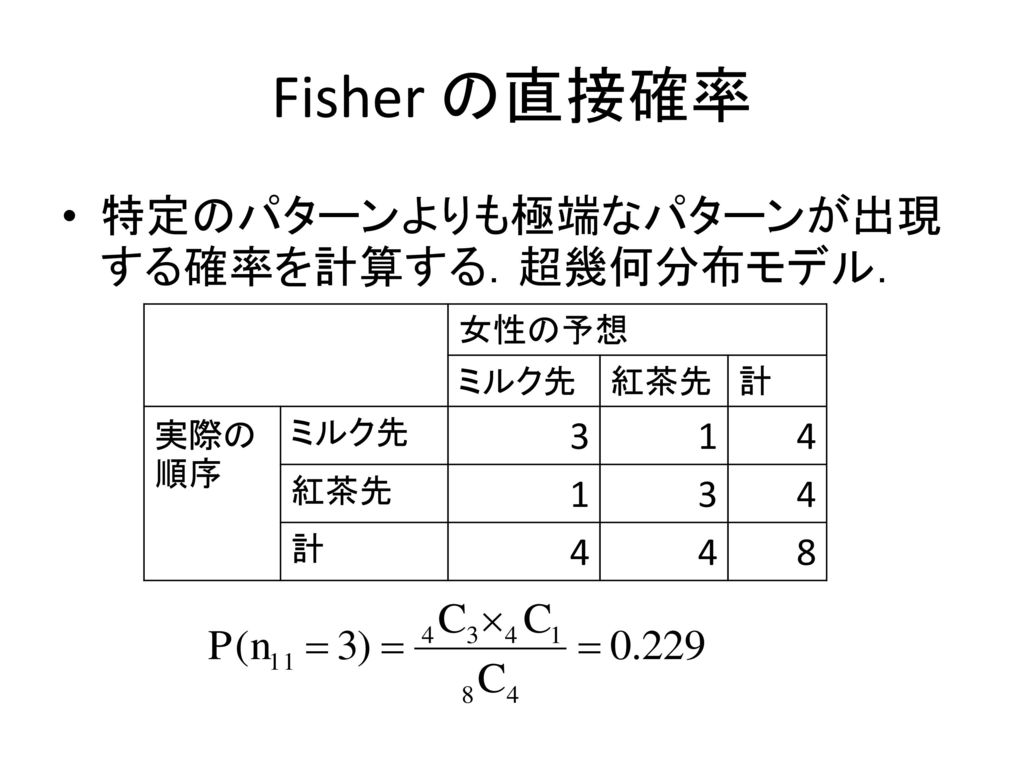



寺尾 敦 青山学院大学社会情報学部 Fisher の直接確率法 寺尾 敦 青山学院大学社会情報学部 Ppt Download




Spssでx二乗検定をやってみる 出力結果の読み方と意味を基本から丁寧に解説します フィッシャーの正確確率検定についても説明します Youtube




Matlab フィッシャーの正確確率検定はカイ2乗検定より本当に正確か Qiita




カイ二乗 X2 とfisherの検定 化審法 動物数 5 Vs 5 7 Vs 7 Or 12 Vs 12を考える Ppt Download




Spssでカイ二乗検定 フィッシャーの正確確率検定との違いやp値の解釈も いちばんやさしい 医療統計



Rを使った分析 カイ2乗検定 外国語教育研究ハンドブック外国語教育研究ハンドブック



クロス集計 Spssの使い方




統計一口メモ 第8話 Fisher正確検定は片側 それとも両側 安全性評価研究会
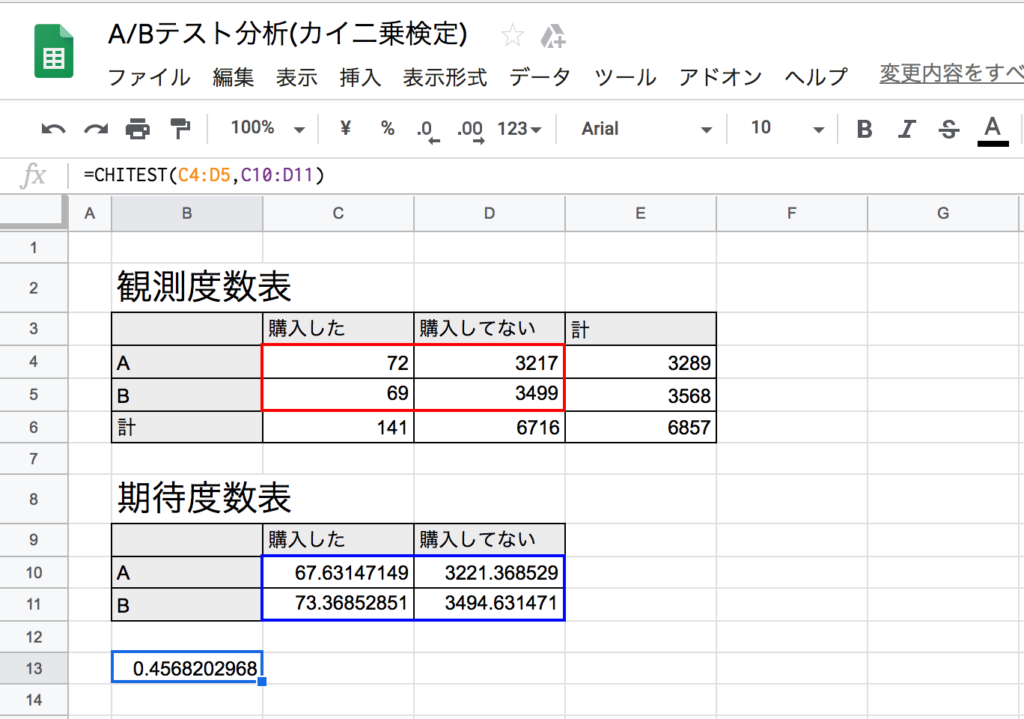



スプレッドシートでピアソンのカイ二乗検定 独立性の検定 を行う方法 たぬハック




フィッシャーの正確確率検定とは カイ二乗検定との違いをわかりやすく いちばんやさしい 医療統計
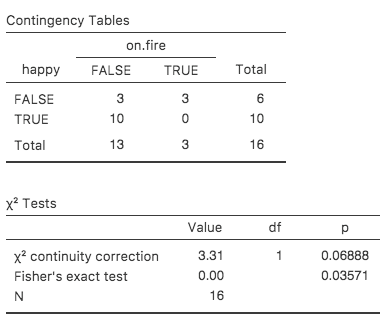



第10章 カテゴリーデータの分析 Jamoviで学ぶ心理統計
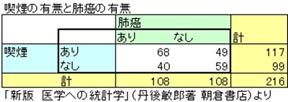



フィッシャーの直接確率検定 統計解析ソフト エクセル統計




Fisherの正確確率検定 Study Channel




第4講 分割表の検定と論文表現



R でフィッシャー正確確率検定をし さらに多重比較を行う方法 高知の田舎で耕すデータサイエンス農家のブログ




Ezrでfisherの正確検定を行う方法 深kokyu



フィッシャーの正確確率検定について教えてください 表は ある病院 Yahoo 知恵袋




医療統計 データ解析しながらいつの間にか基本が身につく本 Stataを使ってやさしく解説 羊土社
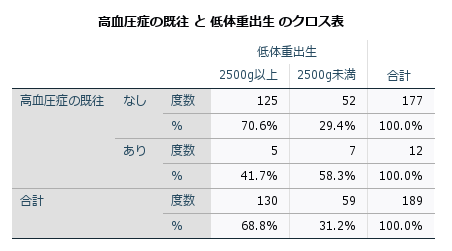



Pearsonのカイ2乗検定 Pearson S Chi Square Test Statsguild Inc スタッツギルド株式会社




Excel Vbaでフィッシャーの正確検定ができる関数を作ってみた2 静粛に 只今統計勉強中



Jmpでカイ二乗検定を実施する方法 フィッシャーの正確確率検定も いちばんやさしい 医療統計




統計 Fisher S Exact Test こちにぃるの日記




フィッシャーの正確確率検定 For Android Apk Download




カイ二乗 X2 とfisherの検定 化審法 動物数 5 Vs 5 7 Vs 7 Or 12 Vs 12を考える Ppt Download



統計初心者です フィッシャーの正確確率検定でエクセルでp値を求めたら1 00 Yahoo 知恵袋




第4講 分割表の検定と論文表現




寺尾 敦 青山学院大学社会情報学部 Fisher の直接確率法 寺尾 敦 青山学院大学社会情報学部 Ppt Download



スポーツ健康科学部ブログ あいコアの星 立命館大学



Ezrでカイ二乗検定とフィッシャーの正確検定の実施方法 分割表でクロス集計 いちばんやさしい 医療統計




Fisherの正確確率検定 薬剤師の備忘録




事例136日出学園中学校 高等学校 第12回全国高等学校情報教育研究会全国大会 キミのミライ発見




医療統計 データ解析しながらいつの間にか基本が身につく本 Stataを使ってやさしく解説 羊土社




クロス集計表で独立性検定のカイ2乗検定を行いましたが いくつかのセルは期待度数が5未満ですと表示されてしまいます




2値データの解析 2 Fisherの正確検定 統計学入門一歩先へ



カイ2乗検定と Fisherの正確検定チュートリアル Xlstat Support Center
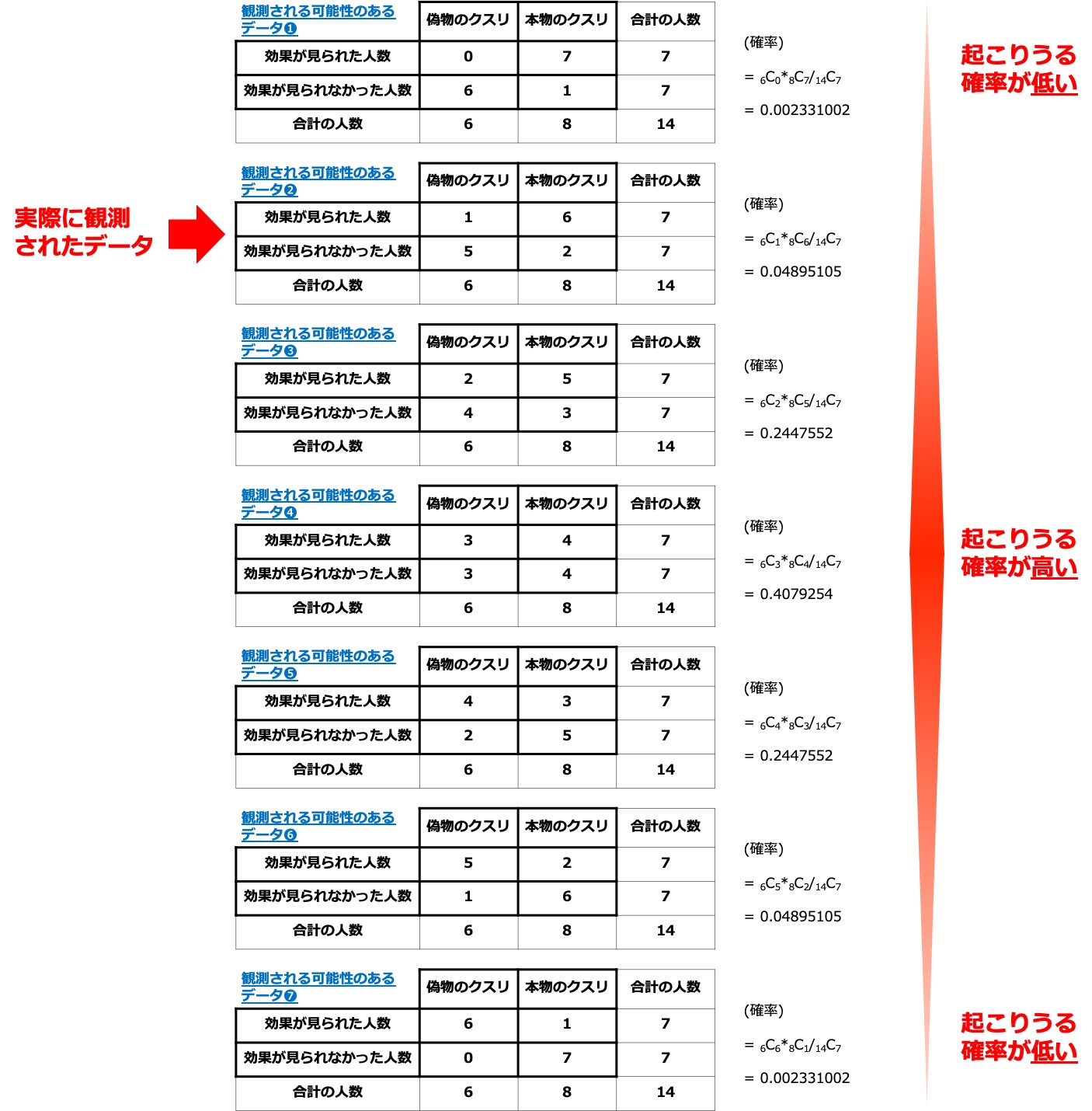



フィッシャーの正確確率検定をわかりやすく解説 Rを使って検定 Mi Chan Nel みっちゃんねる




フィッシャーの正確確率検定 情報リテラシー
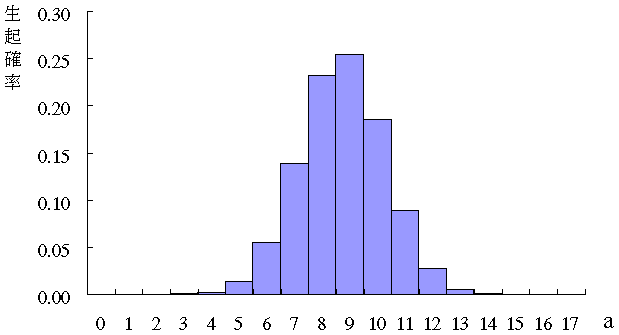



フィッシャーの正確確率検定とは何 Weblio辞書



Ezrの使い方 カイ2乗 X2 検定 フィッシャーの正確検定 気楽な看護 リハビリlife
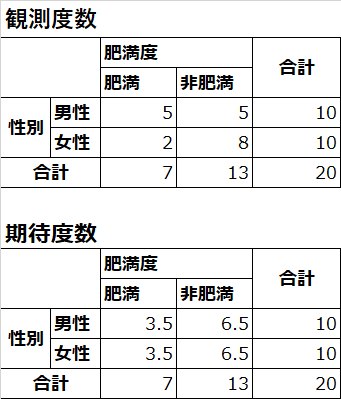



R 栄養統計 性別と肥満度に関係があるか カテゴリデータの栄養統計 みんな栄養に頼りすぎてる
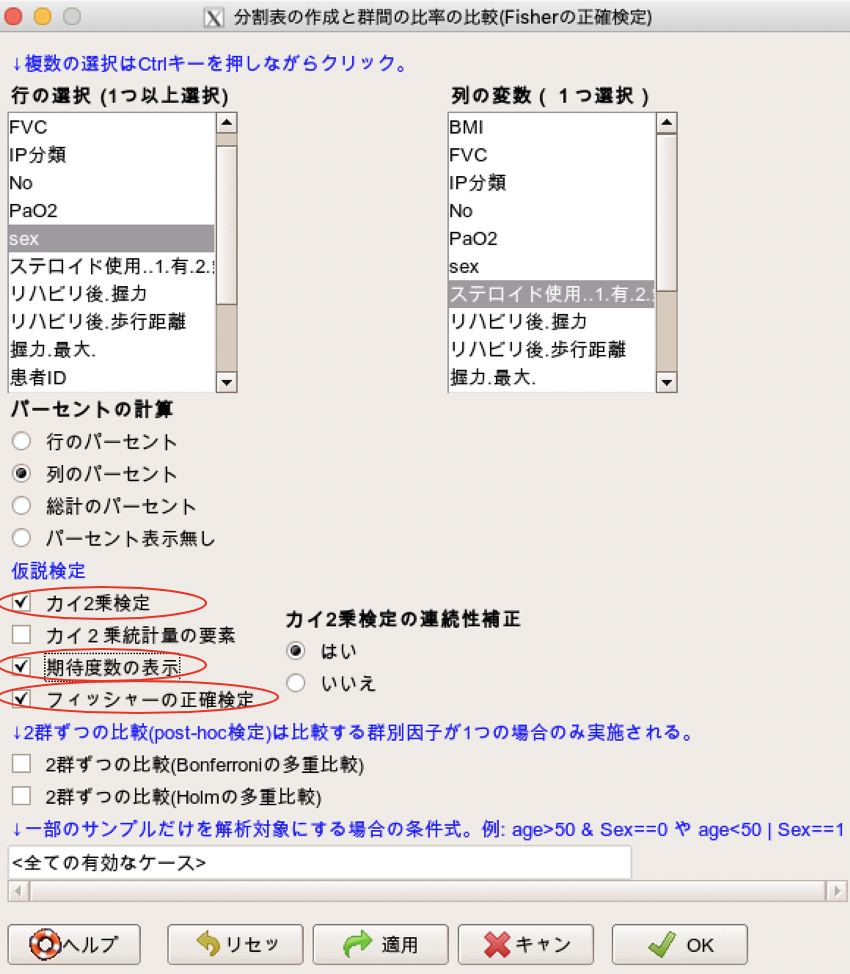



Ezrの使い方 カイ2乗 X2 検定 フィッシャーの正確検定 気楽な看護 リハビリlife



フィッシャーの正確確率検定
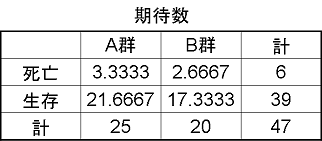



X2乗検定とfisher正確確率検定 X2乗検定の不適切使用をしていませんか Earlの医学ノート
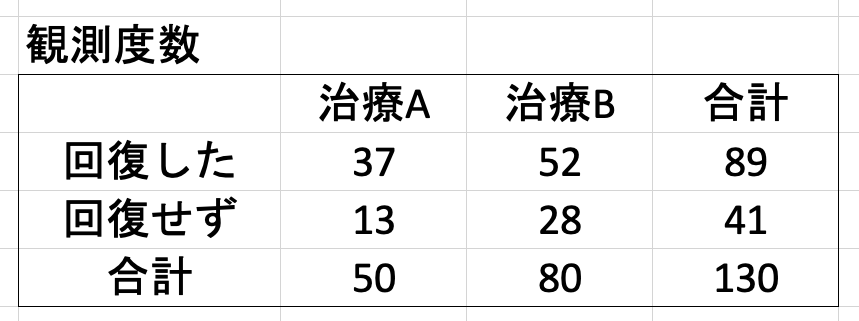



カイ二乗検定 独立性の検定 原理と Excel による解析




Ezrでカイ二乗検定とフィッシャーの正確検定を実施する方法 Youtube



カイ二乗検定結果 書き方



スポーツ健康科学部ブログ あいコアの星 立命館大学




カテゴリデータの関係性を検定 Excelでできるカイ二乗検定 オッズ比も紹介 2年でデータサイエンティストになった人が教える 初心者のためのai データ分析




黒木玄 Gen Kuroki 数楽 統計 Fisherの正確確率検定は周辺度数が固定されている特殊な場合しか全然正確 ではないし Fisherの正確確率検定に近付けるためにyates連続性補正をしたカイ二乗検定を周辺度数が固定されていない場合以外に使うのは誤り という




独立性のカイ二乗検定 例題を用いてわかりやすく解説 Avilen Ai Trend
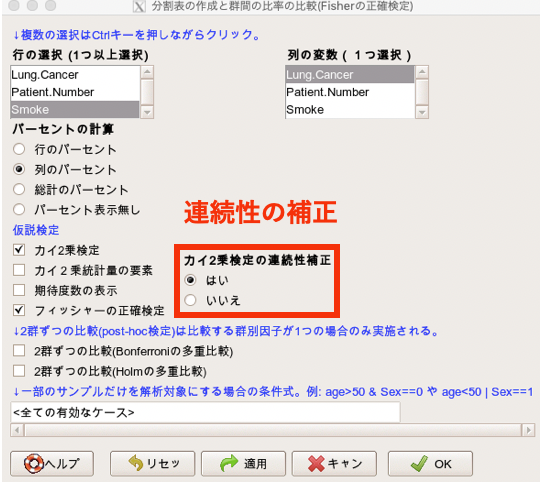



Ezrでカイ二乗検定とフィッシャーの正確検定の実施方法 分割表でクロス集計 いちばんやさしい 医療統計




Ezrでカイ二乗検定とフィッシャーの正確検定の実施方法 分割表でクロス集計 いちばんやさしい 医療統計




Ezrでfisherの正確検定を行う方法 深kokyu




Fisherの正確確率検定について質問です Jmpという統計ソフトを用い 統計学 教えて Goo




Excel Vbaでフィッシャーの正確検定ができる関数を作ってみた1 静粛に 只今統計勉強中




Spssでカイ二乗検定 フィッシャーの正確確率検定との違いやp値の解釈も いちばんやさしい 医療統計
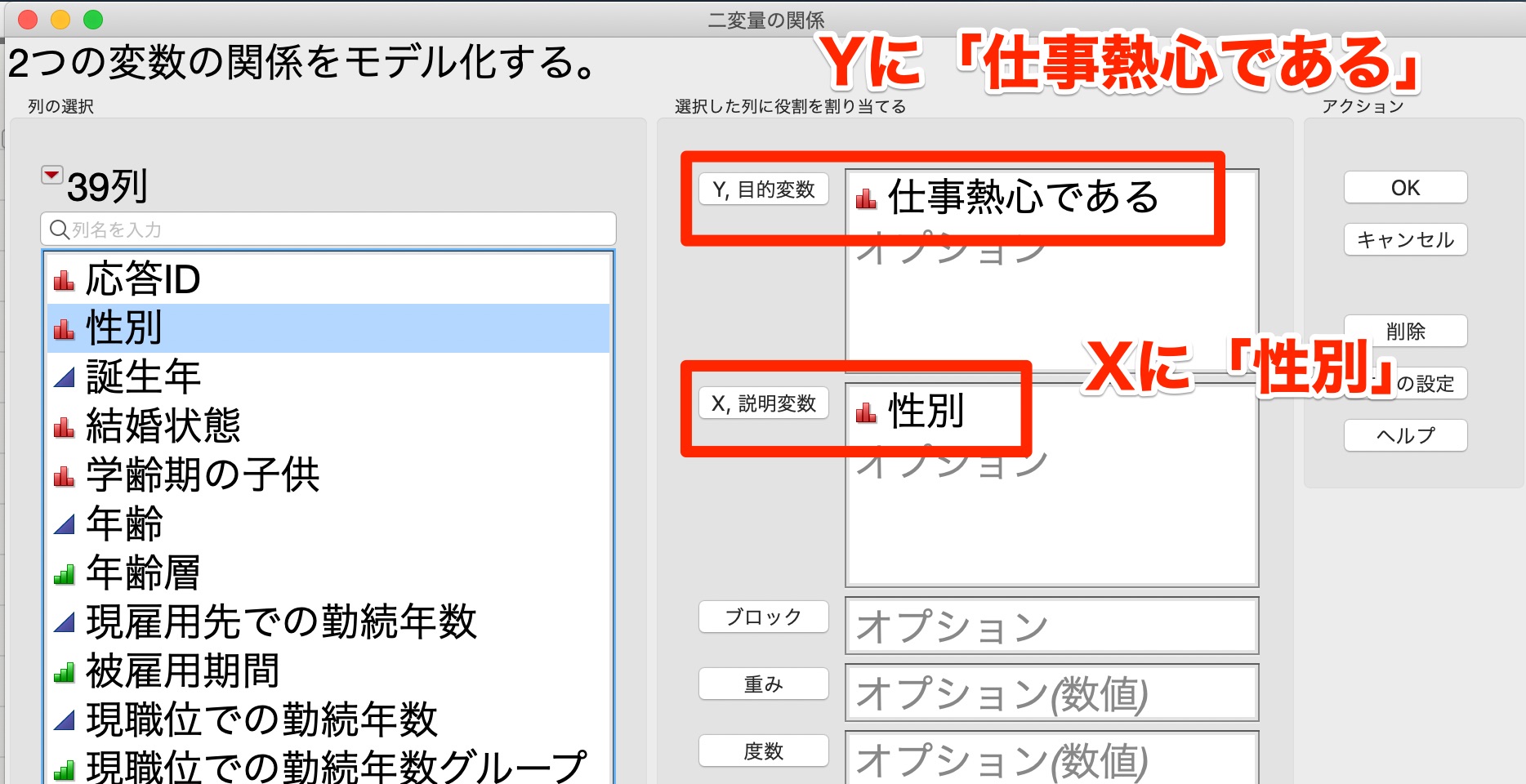



Jmpでカイ二乗検定を実施する方法 フィッシャーの正確確率検定も いちばんやさしい 医療統計



検定結果の解釈




統計一口メモ 第8話 Fisher正確検定は片側 それとも両側 安全性評価研究会
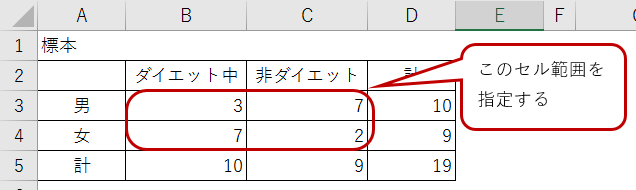



Excel Vbaでフィッシャーの正確検定ができる関数を作ってみた2 静粛に 只今統計勉強中
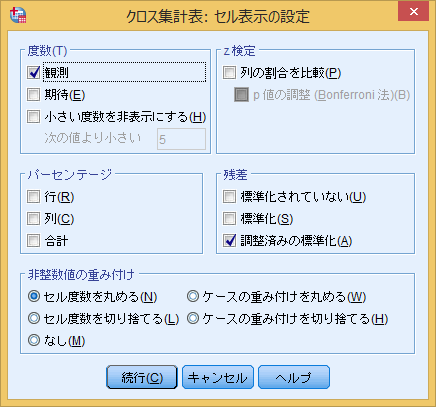



Spssでカイ二乗検定 フィッシャーの正確確率検定との違いやp値の解釈も いちばんやさしい 医療統計




統計手法の選択 伊藤慎也 いとうしんや のページ
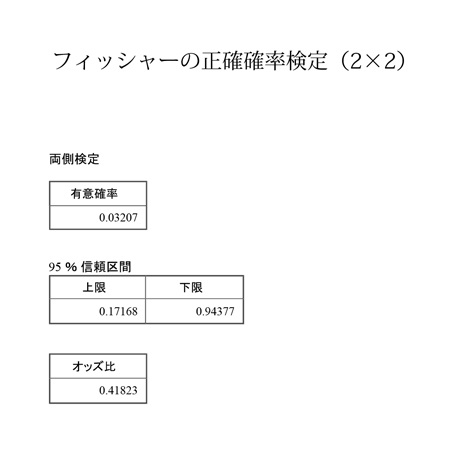



分割表の検定 統計学活用支援サイト Statweb




独立性のカイ二乗検定 例題を用いてわかりやすく解説 Avilen Ai Trend



Spssを用いたカイ2乗検定 X2検定 カイニ乗検定 の方法 フィッシャーの直接確率 残差分析とは 素人でもわかるspss統計




生き残り 百 通常 フィッシャーの検定 Uniqpro Jp




フィッシャーの正確確率検定とは カイ二乗検定との違いをわかりやすく いちばんやさしい 医療統計




Fisherの直接検定のやり方 実験データの具体的な解析方法
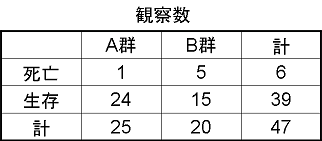



X2乗検定とfisher正確確率検定 X2乗検定の不適切使用をしていませんか Earlの医学ノート




フィッシャーの正確確率検定をわかりやすく解説 Rを使って検定 Mi Chan Nel みっちゃんねる




Ezrでカイ二乗検定とフィッシャーの正確検定を実施する方法 Youtube




遺伝統計学 夏の学校 大阪大学17講義資料 統計学入門
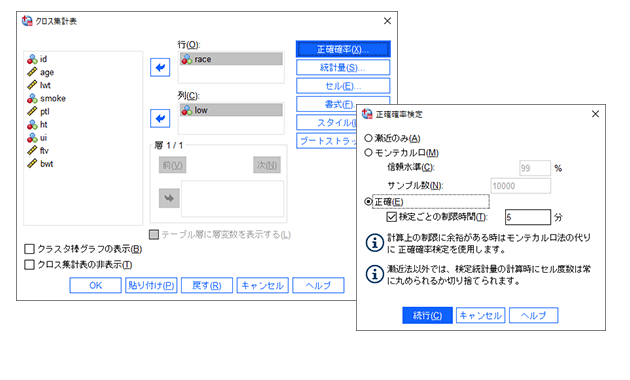



Ibm Spss Exact Tests 製品情報 小サンプルでの正確有意確率
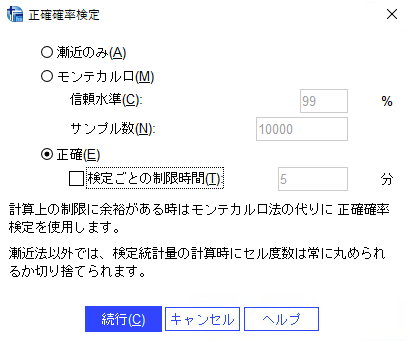



クロス集計表で独立性検定のカイ2乗検定を行いましたが いくつかのセルは期待度数が5未満ですと表示されてしまいます




フィッシャーの正確確率検定 For Android Apk Download


